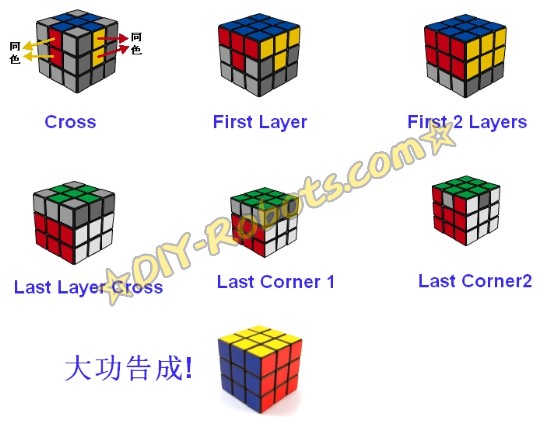
解魔方的机器人攻略28 – 总结
由 动力老男孩 发表于 2010/06/05 21:48:08经过这么长的时间,终于把萝卜头的制作攻略全部发完了。这次发攻略的过程,我把萝卜头重新搭建了一遍,把所有的代码也整理重写了。新版的小萝卜头看上去更好看一点(个人感觉,呵呵),代码容错能力也强了很多。现在在各种不同的灯光条件下,基本都可以正确识别颜色,并且转动过程中,魔方掉下来的情况也很少见了。终于松了一口气,对博客和对萝卜头都算有一个交代了。
我家圈圈很快就要降生,接下来的一段时间博客可能会很少更新。小爱的进度看来已经远远落后,目前还只是一个可以用手机遥控的小车。不过来日方长,我会继续制作并且和大家分享的。
下面转几个国外达人制作的魔方机器人,其中最快的已经可以在十秒左右解出魔方。据说人类的世界记录是7秒多,有志于突破人类极限的朋友,可以参考参考,我非常愿意为此贡献一点力量。
世界最快的乐高魔方机器人

目前最快的魔方机器人
作者把视频发在了youtube上,无法转载,有兴趣的同学请自行翻墙过去看看:
http://www.youtube.com/user/RoboticSolutions
介绍文章:
http://singularityhub.com/2010/02/17/lego-robot-solves-any-rubiks-cube-in-less-than-12-seconds-video/
五阶魔方机器人
用的也是Lego studio摄像头+NXT,5阶魔方还原算法自然是这个机器人的核心,但并非lego范畴,这里可以看到David Gilday愈加成熟的PC端处理程序,看起来相当酷。此外玩过多阶魔方的朋友都知道,这种魔方的翻转定位是最大的问题,所以这款机器人采用了一个相对丑陋的框式造型来帮助解决这个问题,气势上差了一点,但毕竟是第一款,6分43秒185步的测试水平也算世界纪录了。
视频地址
URL:
http://www.tudou.com/programs/view/HXeCwaDdXW0/
大型魔方机器人
大型机械臂,从取魔方,识别,到翻转,放回,仿佛可以看见不远将来家里的小机器人接过你随手拧乱的魔方,咻咻复原的可爱场景。
视频地址:
URL:
http://www.tudou.com/programs/view/TLuTp8mWLPM/
四阶魔方机器人
这是一款用NXT+N95手机的魔方机器人,旋转的结构很酷:
http://blog.izxg.com/?tag=%E4%B9%90%E9%AB%98